According to World Health Organization, by 2020, approximately 32 million cataract surgeries will be performed globally on a yearly basis (1). It is the most performed surgery in ophthalmology and remains as the ultimate refractive surgery. Cataract surgery is not only a way to improve a patient’s visual acuity, but it is an opportunity to help them achieve a state of spectacle independence. Meticulous attention to detail is given to the several necessary pre-, intra-, and post-operative steps to help achieve these goals. To almost all cataract surgeons, achieving the desired post-operative refractive outcome is of utmost importance. Surgeons aim to maximize accuracy and limit post-operative refractive irregularities in order to help patients achieve their desired post-operative refractive needs and desires.
Following cataract surgery, the resulting two-lens system of the cornea and the intraocular lens (IOL) in large part determines a given patient’s post-operative refraction. This makes the choice of picking the most appropriate IOL one of the most important steps in cataract surgery. This matter is largely guided by an individual surgeon’s discretion and personalized and experiential preferences in choosing an IOL for a given eye. A lens is chosen based on a suggested IOL power from one of the modern IOL calculation formulas preferred by the surgeon. In today’s cataract surgery, there are far more measures to optimize and improve this process than ever before. This abundance in choice, however, is often cause for clinical dilemmas and confusion when it comes to targeting an optimal post-operative refraction for a given patient.
IOL calculations have evolved greatly since the early days of the first- and second-generation IOL formulas. In the modern-day demanding landscape, a generally accepted goal for a post-operative refractive outcome is to be within 0.50 D of emmetropia or slight myopia. However, in reality this goal is only achieved approximately 70–80% of the time with any one unoptimized formula (2). This leaves approximately one out of four patients greater than 0.50 D off of targeted refraction. This refractive variance may then lead to a need for significant spectacle correction or further surgery to address remaining refractive error. There is a lack of a single, perfect IOL calculation formula or solution which could help minimize such errors and address both the “average” eyes and those with extreme ranges of keratometry and axial length.
Given this paucity, most surgeons rely on multiple formulas to calculate lens power for their upcoming surgeries. This process often requires dedication of a significant portion of clinical workflow and time to decide on a preferred IOL calculation solution and commit to a lens implant choice. The desire to simplify this process and arrive at a more accurate IOL calculation framework has led to the development of the next generation of IOL formulas.
The modern IOL calculation formulas have greatly evolved from the simple linear regression formulas such as the SRK I and SRK II (3). Introduction of theoretical formulas such as the Holladay, SRK/T, Hoffer Q, and Haigis provided an improved level of accuracy for many years (4-7). However, more recently, there has been an influx of new formulas. Recently the Barrett, Olsen, Holladay 2, and the Hill-RBF formulas have been introduced. Further, many of these formulas have been optimized over the years and have supplemental adjustments to help hone their accuracy (8). While these sophisticated formulas are far better than the previous generations’ regression formulas, each formula has its own advantages and limitations under specific circumstances. There exists no single formula which is adaptable and malleable enough to be applicable for all types of eyes.
In 2015, Ladas et al. devised a solution to address this need by introducing the concept of an IOL ‘super formula’ (9). Although previous generations of IOL formulas were thought of as two-dimensional algebraic equations, Ladas et al. found a novel methodology of depicting these formulas in three dimensions (Figure 1). Doing so provided a framework to analyze these formulas in three dimensions and observe areas of nuance where they are similar or different. Based on this and peer-reviewed literature, the best portions of each of the modern IOL formulas were chosen and an IOL ‘super surface’ was developed based on an amalgam of these formulas. From this super surface, the ‘super formula’ was derived.
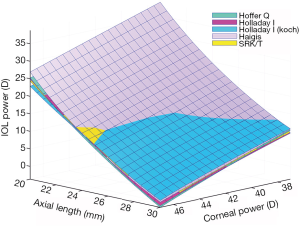
The assembly of this formula required careful inspection of at least five of the modern IOL formulas (Hoffer Q, Holladay I, Holladay I with Koch adjustment, Haigis, SRK/T) (4-8). Each of these formulas have their unique set of advantages and limitations. Portions of each formula were included and excluded depending on how suitable they were deemed for a particular ‘eye’ in peer-reviewed literature. For example, retrospective analyses have shown that while the SRK/T tends to be better for longer eyes, very short eyes may do better with the Hoffer Q (8). Some eyes require more nuance and optimization. For example, shorter eyes are difficult to calculate as the smallest of changes in the estimated lens position (ELP) can alter the lens power calculations drastically because of the delicate interplay between the vergence and ELP calculations.
The ultimate benefit of the super formula is that it is usable for all types of eyes: short or long, flat or steep. The concept of three-dimensionality that is innate within the super formula and its depicted super surface serves as a graphical method of comparing one or more formulas. Doing so has led to further refinement of the super formula by highlighting areas of clinic dilemmas and clinical agreement between one or more formulas. Next, the use of this formula promises to take the burden away from the surgeon of having to deal with multiple formulas leading up to the next surgery day. It offers itself as a single solution which hopes to address eyes with average corneal power and axial length values, and those that are of anomalous extremes. Lastly, and perhaps more importantly, it provides a malleable framework which allows for targeted improvement within the formula.
The formula as published served as a solid backbone to what is now an advanced version of this formula. In its original state, it used axial length, corneal power, anterior chamber depth, lens constant and target refraction values as input parameters. With the help of complex deep learning techniques and artificial intelligence, this formula has evolved to an improved level of accuracy. The latest iteration of the formula is optimized using actual post-operative outcomes taken from several high-volume cataract surgeons. This optimization process applies a unique adjustment to an eye based on its axial length, corneal power, and anterior chamber depth. Using this ‘big data’ methodology may help achieve a higher level of accuracy in eyes with anomalous parameters, such as those with a flat or steep cornea, long or short axial length, deep or shallow anterior chamber, or other parametric variations. This methodology has helped to significantly minimize the ‘delta’ between the predictions made by the formula and actual post-operative refractive outcomes.
The next step in further perfecting this approach is to include more variables and to hone the accuracy further. Any number of IOL formulas and variables from the past or the future can be incorporated in some fashion and extent into the super formula algorithm. Several aspects of the formula may be optimized further based on actual post-operative outcome data and via introduction of additional parameters (such as posterior corneal power and anterior chamber depth). The super formula provides a framework consisting of the best of all the modern IOL solutions. Further, it is a flexible and malleable algorithm which can be trained and developed to yield increasingly accurate solutions. This big data and ‘crowd sourced’ approach could one day use millions of data points to achieve unprecedented levels of accuracy. This approach can evolve over time and become a system or a ‘living organism’ that never ceases to improve.
The future of IOL calculations is promising. The desire to achieve supreme post-operative refractive outcomes is responsible for the continued growth spurt in the industry of IOL calculations. The super formula framework in particular may be applicable in the near future to other relevant aspects of IOL calculations such as post-refractive, toric, and pediatric cataract surgeries. With continued deployment of advanced mathematical techniques, artificial intelligence, precise biometric instruments, and introduction of additional variables, the process of IOL calculations can reach new heights of accuracy and simplicity.